Niveau

x Facile

xx Moyen

xxx Difficile

1 - Le pliage de Mathias x

À l’aide de la feuille de papier rectangulaire representée ici,

Mathias a réalisé la forme représentée suivante.

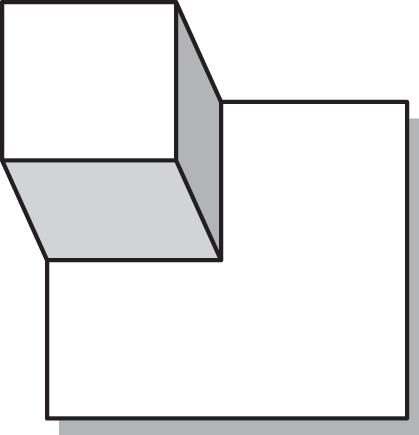
Il a seulement donné deux coups de ciseaux, il a fait trois plis et il n’a rien jeté.

Sur le dessin de la feuille de papier, indiquez par des traits continus l’emplacement des coups de ciseaux, et par des traits en pointillés l’emplacement des plis.

2 - La bande de papier x

Découpez une longue bande de papier en forme de rectangle. Pliez cette bande une fois, en deux parties égales, puis dépliez la bande ; vous visualisez un unique pli. Pliez une autre bande deux fois de suite, puis dépliez la bande; vous voyez maintenant trois plis.

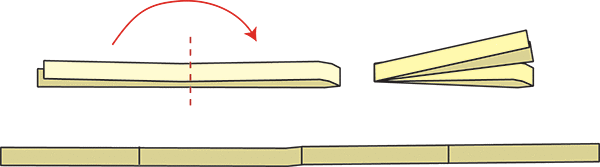
En supposant que l’on puisse plier une bande de papier n fois de suite selon la même méthode, combien de plis verrait-on en la dépliant ?

3 - Chorégraphie géométrique xx

Les figures ci-contre montrent les différentes étapes d’une suite de pliages.

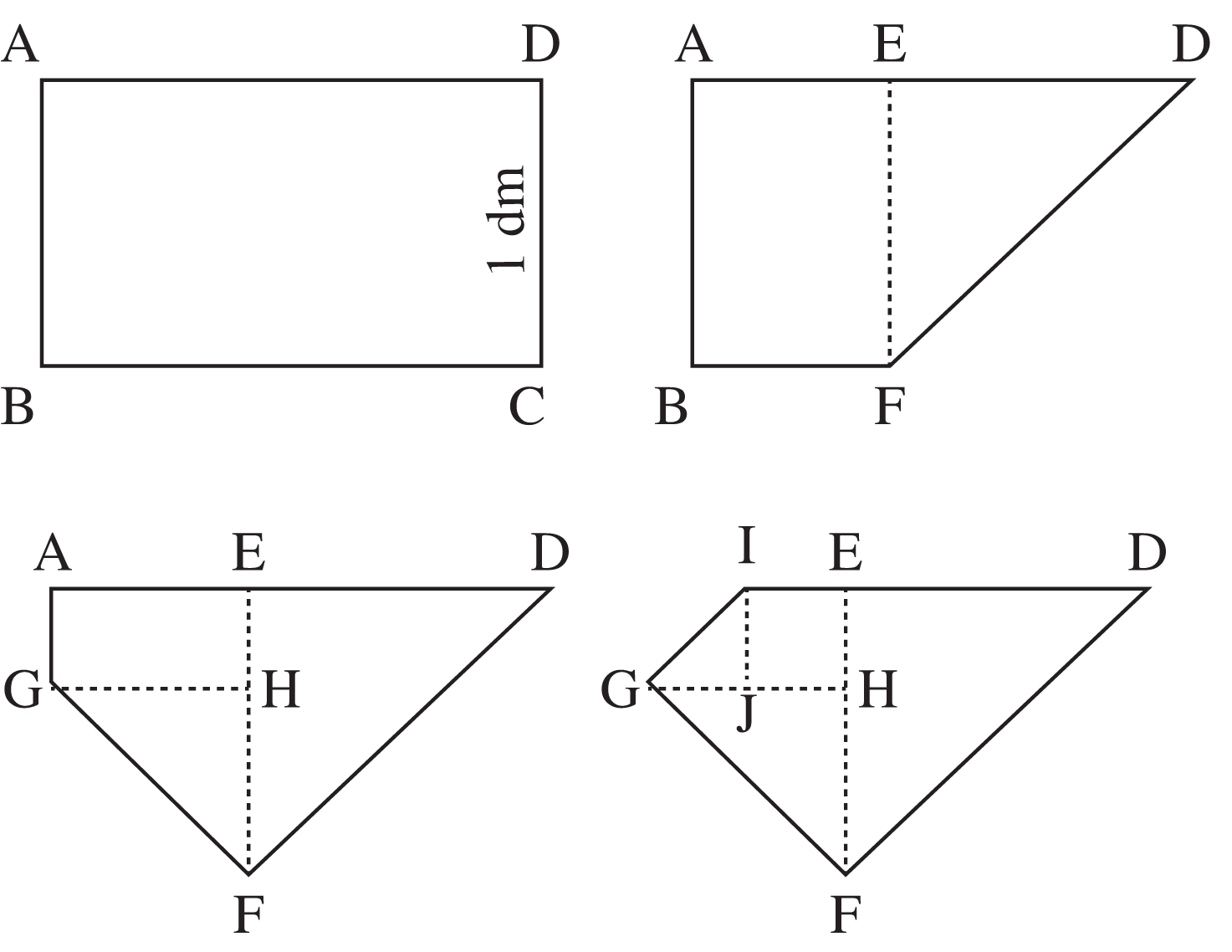
À partir d’un rectangle ABCD, on a d’abord fait un pli [DF] en amenant le point C du rectangle initial sur le côté [AD]. On a ensuite fait un pli [GF] en amenant le sommet B sur le segment [EF]. On a finalement réalisé un pli [GI] en amenant le sommet A sur le segment [GH].

Le rectangle initial avait une largeur égale à 1 dm et le pli [GI] a une longueur égale à √2 / 5 dm.

Quelle était la longueur du rectangle initial ?

4 - Le rectangle plié xx

Un rectangle de papier est plié comme l’indique la figure, de telle sorte que son sommet supérieur gauche vienne en D sur le côté [AB]. On sait que AB = √2 dm et que BC = 1 dm.

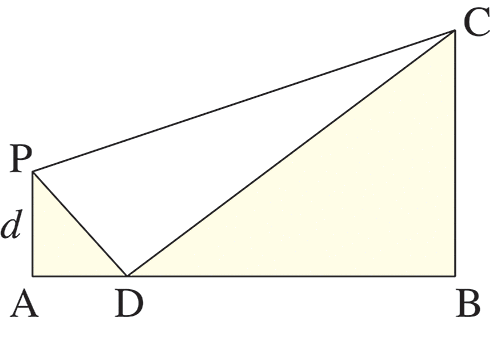
Quelle est la longueur AP ?

5 - Suivant les pointillés… xx

Un triangle est plié le long de la ligne pointillée rouge, comme le montre la figure. L’aire du triangle initial est 1,5 fois plus grande que l’aire totale de la figure obtenue après pliage.

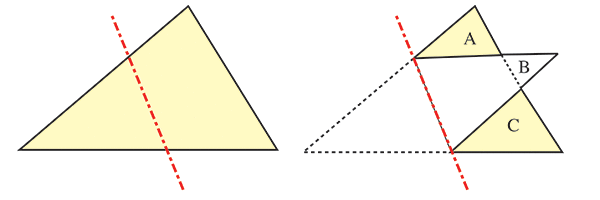
Sachant que la somme des aires du triangles A, du petit triangle B et du triangle C vaut 1 dm², quelle est l’aire du triangle de départ ?

6 - Le carré qui se met en quatre xxx

Un carré de papier de 1 décimètre de côté est plié selon le segment [VR]. Le sommet en bas à droite vient en P sur le côté supérieur, comme le montre la figure, en créant les trois triangles PQR, TPS et SUV.

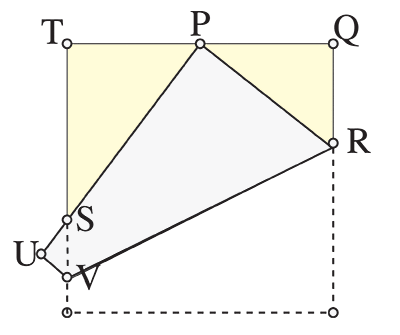
Si P est le milieu de [TQ], quelle est la longueur du segment [QR] ? Quelles sont les longueurs des côtés du triangle SUV ?

7 - Le triangle et toute sa bande xxx

Une bande de papier est constituée de vingt-huit triangles équilatéraux identiques.

En effectuant des plis de cette bande uniquement selon les côtés des triangles équilatéraux et en replaçant après chaque pli la bande pliée dans un plan (certaines parties de la bande présentant alors plusieurs épaisseurs de papier), est-il possible de faire coïncider les segments [AB] et [CD] ?

8 - Une construction pointilleuse xx

On plie un rectangle de longueur 24 cm selon un segment [AB], comme l’indique la figure, de façon que le sommet S vienne exactement se superposer avec le sommet T.

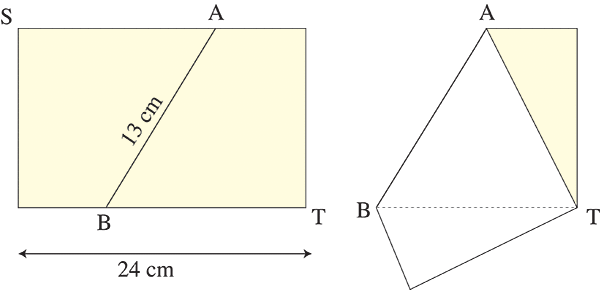
On sait que la longueur du pli est égale à 13 cm.

Quelle est la largeur du rectangle initial ?

9 - Une mise en plis qui défrise xxx

On plie un triangle équilatéral de côté 15 cm selon un segment [XY] de façon à amener le sommet A en D, sur le côté [BC] à 3 cm de B, comme l’indique la figure.

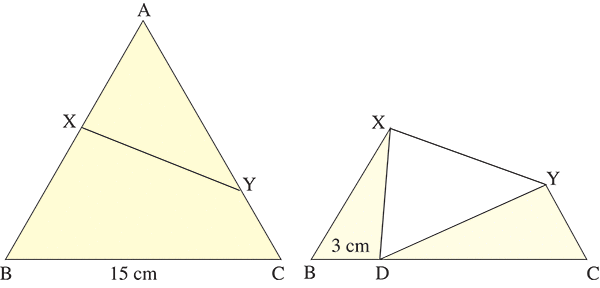
Quelle est la longueur du pli ?